📌 정렬 알고리즘 사용 시 고려할 사항
- 시간 복잡도
- 메모리 사용량
- 안정성 (stability) : 데이터의 순서가 바뀌는지 여부
- 직렬 vs 병렬
💡 안정성을 고려하는 이유 : 모든 정렬 알고리즘은 같은 key를 가진 데이터의 순서를 안 바꾼다고 착각하기 때문이다.
📌 정렬 알고리즘을 선택할 때 고려할 사항
- 정렬할 데이터의 양
- 데이터와 메모리
- 이미 정렬된 정도
- 필요한 추가 메모리의 양
- 상대위치 보존여부 (안정성)
💡 대표적인 정렬 알고리즘의 시간복잡도
| O(n^2) | O(nlogn) |
| Insertion sort ❗️best = O(n) in sorted list ❗️worst = O(n^2) in reverse sorted |
Quick sort ❗️worst = O(n^2) in already sorted list |
| Selection sort | Merge sort |
| Bubble sort | Heap sort |
📎 Bubble sort (버블 정렬)

그림과 같이 j방향으로 비교를 하면서 인접한 두 노드를 비교, swap한다.
이해를 위해 바로 예시를 들자면, i=1일 때(0이지만 편의상 1로)

📌 각 step마다 n-1번의 비교가 일어난다.
📌 이는 총 n steps가 필요하므로 n(n-1) = n^2의 비교가 일어난다.
💡 수행하기는 쉽지만 Insertion sort보다 느리다.
# sudo code for Bubble Sorting
for i <- 1 to length[A]
do for j <- length[A] down to i+1
do if A[j] < A[j-1]
then exchange A[j] <-> A[j-1]int n = 7;
int arr[7] = {8, 4, 6, 9, 2, 3, 1};
for(int i=0; i<n; i++) {
for(int j=n-1; j>=0; j--) {
if(arr[j] < arr[j-1]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
⏱️ 시간복잡도 계산
- 비교 횟수
- best, worst, common 모든 경우 동일
- n-1, n-2, ... 1 번 = n(n-1) / 2
- 교환 횟수
- 역순으로 정렬되어있는 경우엔 swap 함수 작업으로 3번의 이동 (비교횟수 * 3) = 3n(n-1)/2
- 이미 정렬된 경우 이동 발생 X
- T(n) = n(n-1)/2 = O(n^2)
📎 Insertion sort (삽입 정렬)
: 작은게 나올 때까지 비교하다가 삽입하는 정렬, bubble sort보다 빠름
모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입한다.
( 배열은 sorted, unsorted 두개의 sub-arrays로 나뉜다. )
Key값(unsorted array의 첫번째 값)은 두번째 원소부터 시작한다.
첫번째 원소는 정렬되어있는 상태로 친다.

// sudo code for Insertion sort
for j <- 2 to n
do key <- A[j]
i <- j-1 //sorted array 마지막 원소와 비교함
while i>0 and A[i] > key
do A[i+1] <- A[i]
i <- i-1
A[i+1] <- key //key < A[i]일때 swap, i-1로 이동해서 또 비교함
int n;
int i, j, key;
int array[n];
for(j=1; j<n; j++) {
key = array[j];
for(i=j-1; i>=0 && array[i]>key; i--) {
array[i+1] = array[i]; //한칸 뒤로 이동
}
array[i+1] = key; //key값 삽입
}
⏱️ 시간복잡도 계산
- Best case (sorted list)
- 비교횟수
- 이동 없이 1번의 비교만 이루어짐
- 외부 루프 : n-1번
- Best case T(n) = n-1 = O(n)
- 비교횟수
- Worst case (reverse sorted list)
- 비교 횟수
- 외부 루프 안의 각 반복마다 i번의 비교 수행
- 외부 루프 : (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2
- 교환 횟수
- 외부 루프의 각 단계마다 i+2번의 이동 발생
- n(n-1)/2 + 2(n-1) = O(n^2)
- Worst Case T(n) = O(n^2)
- 비교 횟수
💡 거의 sorted 된 list에 적합한 방식이다
📎 Selection sort (선택 정렬)
: smallest element에 깃발을 꽂고 배열 첫번째 위치와 swapping
// sudo code for Selection sort
n <- length[A]
for j <- 1 to n-1
do smallest <- j
for i <- j+1 to n
do if A[i] < A[smallest]
then smallest <- i
exchange A[j] <-> A[smallest]
# define SWAP(s, y, temp) ((temp)=(x), (x)=(y), (y)=(temp))
int n;
int i, j, smallest, temp;
int array[n];
for(i=0; i<n-1; i++) { //마지막 숫자는 자동정렬이므로 n-1까지만 수행
smallest = i;
for(j=1; j<n; j++) {
if(array[j] < array[smallest]) smallest = j;
}
//최소값이 자기자신인지 확인 후 exchange, 아니라면 그대로 둠.
if(smallest != i) SWAP(array[i], array[smallest], temp);
}⏱️ 시간복잡도 계산
- 비교 횟수
- 두개의 for 루프 실행
- 외부 루프 : n-1번
- 내부 루프 : n-1, n-2, ... 1 번 = n(n-1) / 2
- 교환 횟수
- 외부 루프 실행 횟수와 동일. n-1번
- 한번 교환하기 위해선 3번의 이동이 필요하기 때문에 결론적으로 3(n-1)번
- T(n) = n(n-1)/2 = O(n^2)
📎 Quick sorting (분할 정복)
📌 divide & conquer 알고리즘의 예시 중 하나이며 pivot값(주로 배열의 첫번째)을 이용해서 정렬한다.
왼쪽->오른쪽 방향을 low방향, 오른쪽->왼쪽 방향을 high 방향이라고 할 때,
pivot 값을 기준으로 양 끝값에서 low 방향은 pivot 값보다 더 큰 값을, high 방향은 pivot값보다 더 작은 값을 찾는다.
📌 만약 low와 high가 값을 찾지 못해 교차된다면 pivot값과 high값을 swap해주어 새로운 pivot값을 설정해준다.
low와 high가 제대로 된 값을 찾았고 low값의 위치 < high값의 위치라면 두개의 값을 swap해준다.
📌 새로운 pivot값이 설정되었다면 이전 pivot값을 기준으로 배열을 분할해서 계속 진행한다.
아래의 그림속 배열을 예시로 들어 설명하자면,
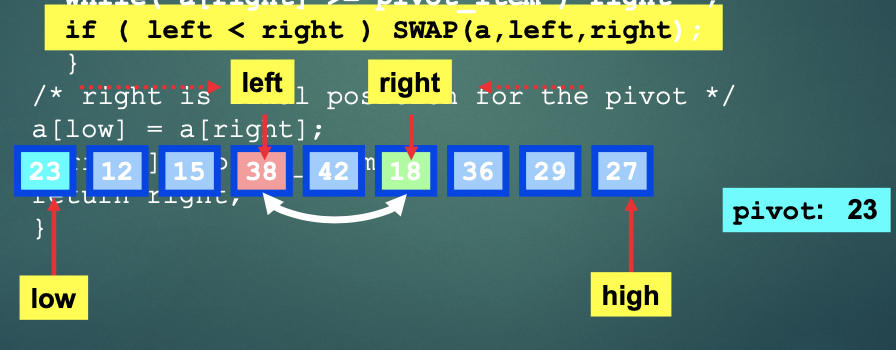
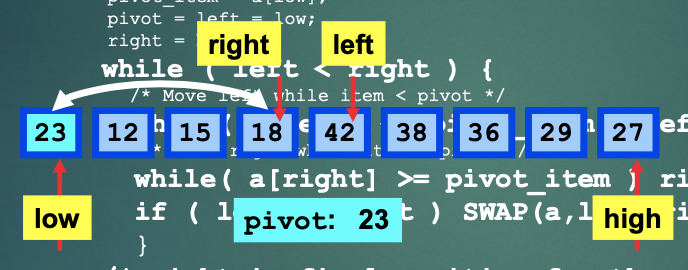
- low방향으로 이동하던 left, high방향으로 이동하던 right가 값을 찾음.
- left값과 right값을 swap 해줌.
- 계속 진행시 left와 right의 위치가 교차됨.
- pivot값과 right 값을 swap해줌.
- 기존 pivot값은 기존 right값 위치에 있음.
- 기존 pivot값을 기준으로 왼쪽 오른쪽, 두개의 배열로 분할해 다시 Quick sort 진행.
=> 각자의 배열에서 첫번째 원소가 새로운 pivot이 된다.
=> 두개의 배열 범위는 (low~right-1), (right+1~high)가 된다.

//sudo code for quick sort
int partition( int *a, int low, int high ) {
int left, right;
int pivot_item;
pivot_item = a[low]; //pivot값을 배열 첫번째 값으로 설정
pivot = left = low;
right = high;
while ( left < right ) { //low와 high가 만나기 전까지
// Move left while item < pivot
while( a[left] <= pivot_item ) left++;
// Move right while item > pivot
while( a[right] >= pivot_item ) right--;
if ( left < right ) SWAP(a,left,right);
}
//right is final position for the pivot
a[low] = a[right];
a[right] = pivot_item;
return right;
}#include <iostream>
using namespace std;
void Swap(int &A, int &B)
{
int Temp = A;
A = B;
B = Temp;
}
void QuickSort(int *arr, int low, int high) {
int pivot = low; // 맨 왼쪽 값을 pivot 설정
int left = low + 1; //맨왼쪽값 pivot이므로 왼쪽 출발 지점= +1
int right = high;
while(left <= right) {
while(arr[left] <= arr[pivot] && left <= high) left++;
while(arr[right] >= arr[pivot] && right > low) right--;
//엇갈린다면 high와 pivot swap
if(left > right) Swap(arr[right], arr[pivot]);
else Swap(arr[left], arr[right]); //아니라면 left, right swap
}
//처음 pivot값 기준으로 분할계산
QuickSort(arr, low, right-1);
QuickSort(arr, right+1, high);
}
int main(void) {
int N = 8;
int arr[] = {8, 15, 5, 9, 3, 12, 1, 6};
Quick(0, N-1);
for(auto a : arr) cout << a << " ";
return 0;
}📌 Quick Sort 알고리즘의 특징
- 장점
- 속도가 빠르다 : 시간복잡도 O(nlogn)을 가지는 다른 정렬 알고리즘에 비교해도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다 : O(nlogn)만큼의 메모리를 필요로 한다.
- 단점
- sorted 리스트에서는 퀵정렬의 불균형 분할에 의해 오히려 시간이 더 걸린다.
- 퀵 정렬의 불균형 분할을 방지하기 위해선 ?
=> pivot선택 시 리스트를 균등하게 분할할 수 있는 데이터로 선택한다. (Ex. 중간값)
⏱️ 시간복잡도 계산
Best case
- 비교 횟수
- 순환 호출 깊이 : n이 2의 거듭제곱이라고 가정했을 때, n=2^3이라면 2^3->2^2->2^1->2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 따라서 n=2^k의 경우, 깊이는 k=log2n이다.
- 각 순환에서의 비교연산은 전체 리스트를 한번씩 비교하므로 O(n)이다.
- T(n) = 순환 호출 깊이 * 각 순환 호출에서의 비교 연산 = nlog2n
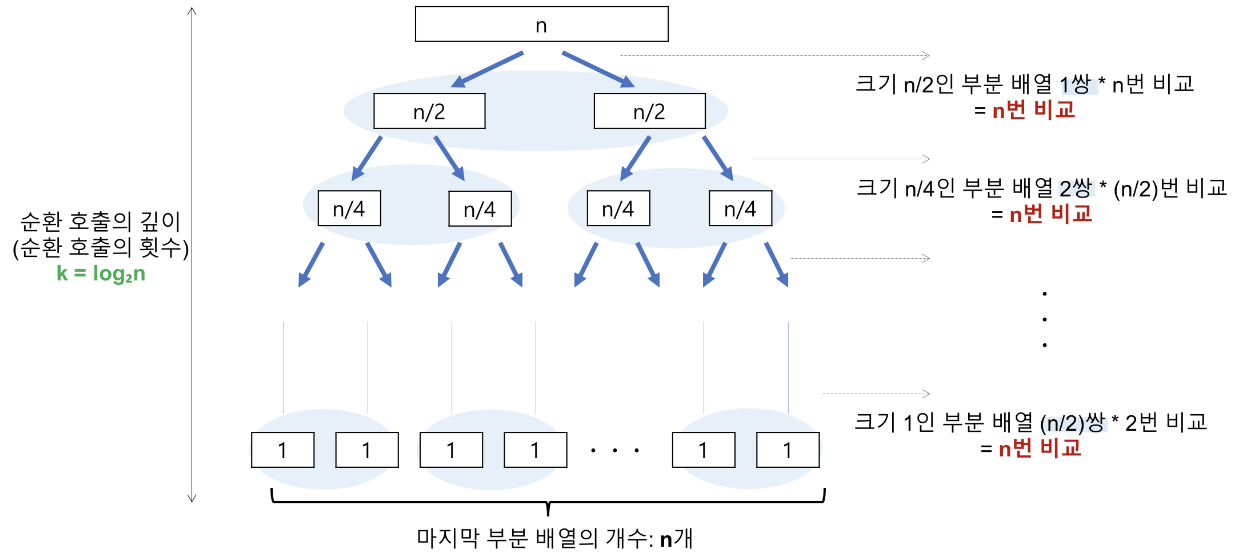
Worst case
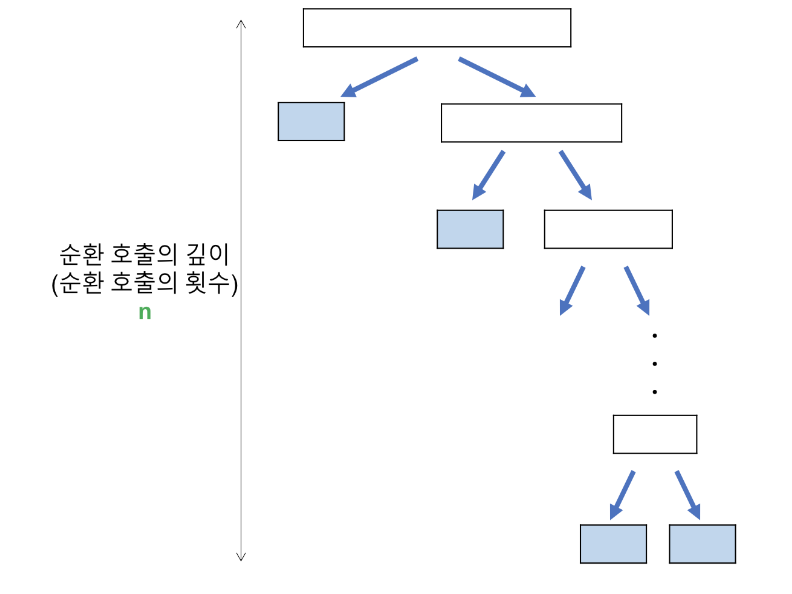
- 리스트가 계속 불균형하게 나눠지는 경우 (특히 sorted list)
- 순환 호출의 깊이 : n
- 각 순환 호출 단계에서의 비교연산 : n
- T(n) = n * n = O(n^2)
📎 Merge Sort (합병 정렬)
: quick sort와 마찬가지로 divide & conquer(분할 정복) 알고리즘의 하나이며, 배열을 항상 반으로 나눈다. => logN 보장됨
즉, 두개의 정렬된 리스트를 하나의 정렬된 리스트로 합병하는 방식이다.
📌 Merge sort는 다음 단계들로 이루어진다.
- 분할 : 입력배열을 같은 크기의 2개의 부분 배열로 분할
- 정복 : 부분 배열을 정렬, 크기가 충분히 작지 않은 경우 순환 호출을 이용하여 다시 분할
- 결합 : 정렬된 부분 배열을 하나의 배열에 합병 => 여기서 정렬이 이루어짐
📌 Merge sort의 과정
- 정렬된 배열을 저장하기 위한 추가적인 리스트가 필요하다.
- 각 부분의 배열을 정렬할 때도 합병 정렬을 순환적으로 호출한다.
- 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병하는 단계에서 이루어진다.
📌 Merge sort 종류
- 반복 합병 정렬 : 입력 리스트를 길이가 1인 n개의 정렬된 서브리스트로 간주
- 첫번째 합병 단계 : 리스트들을 합병하여 크기가 2인 n/2개의 리스트를 얻는다. (홀수일 경우 리스트 하나는 크기가 1)
- 두번째 합병 단계 : n/2개의 리스트들을 다시 합병하여 n/4개의 리스트들을 얻는다.
- 하나의 서브리스트가 남을 때까지 합병을 계속한다.
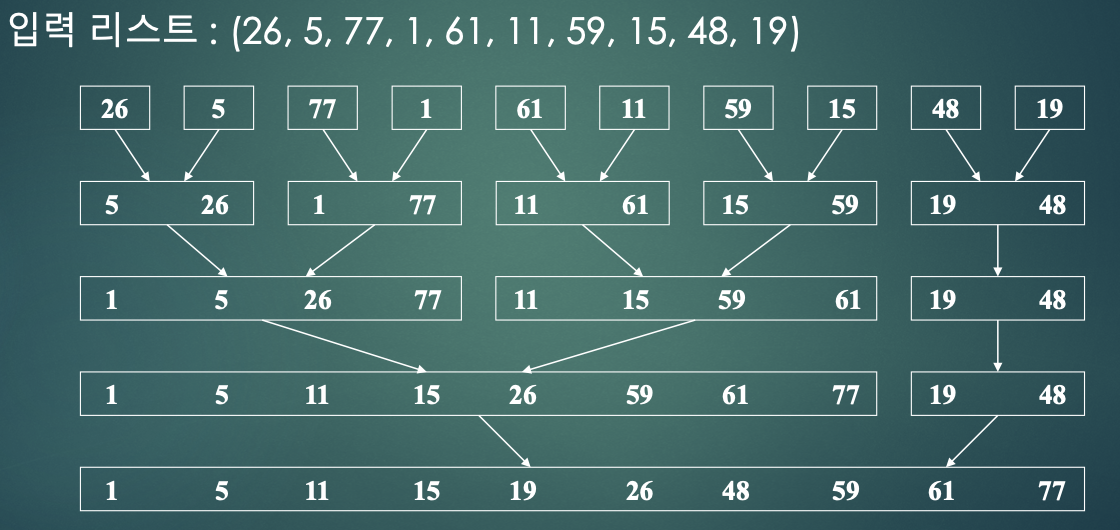
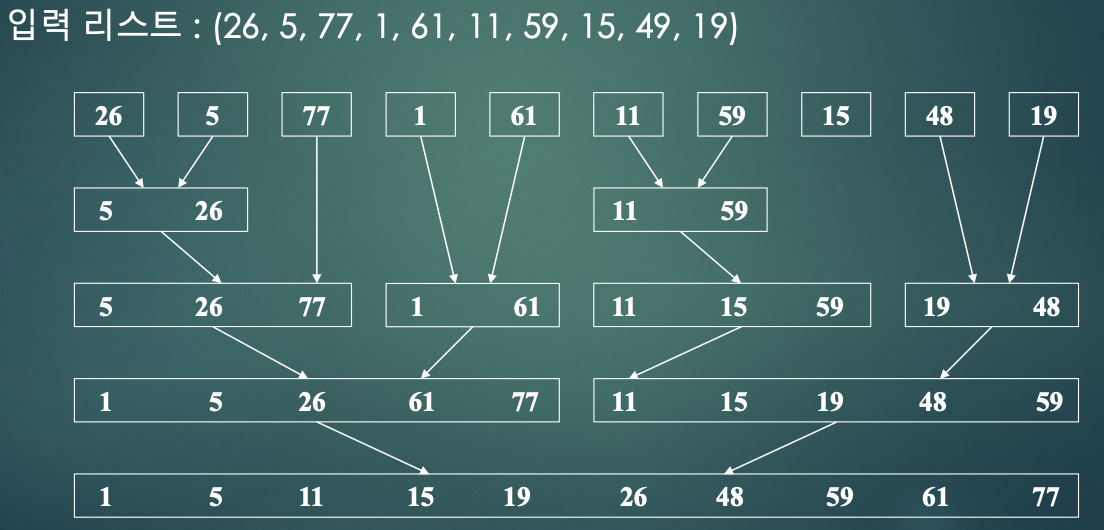
- 순환 합병 정렬 : 정렬할 리스트를 거의 똑같이 두개로 나눈다. (left 서브리스트, right 서브리스트)
- 서브리스트들은 순환적으로 정렬된다.
- 정렬된 서브리스트들은 합병된다.
- 자연 합병 정렬 : 합병 정렬의 변형으로 입력 리스트 내에 이미 존재하고 있는 순서를 고려함
- 이미 정렬되어있는 레코드의 서브리스트들을 식별할 수 있도록 초기 패스를 만들어야 한다.

📎 Heap Sort (힙 정렬)
Merge sort의 문제점 : 정렬한 레코드 수에 비례하여 저장 공간이 추가로 필요하다!
=> Heap Sort는 일정한 양의 저장 공간만 추가로 필요하다.
[참고]
https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
'Algorithm' 카테고리의 다른 글
| [Algorithm] Greedy(탐욕) 알고리즘 (0) | 2023.08.16 |
|---|---|
| [Algorithm] DFS(깊이 우선 탐색), BFS(너비 우선 탐색) (0) | 2023.08.13 |
| [알고리즘] Greedy Algorithm (탐욕 알고리즘) (0) | 2022.10.29 |
| [알고리즘] A* 알고리즘 (0) | 2022.06.10 |
| [C++] KMP 알고리즘 (0) | 2022.05.24 |