728x90
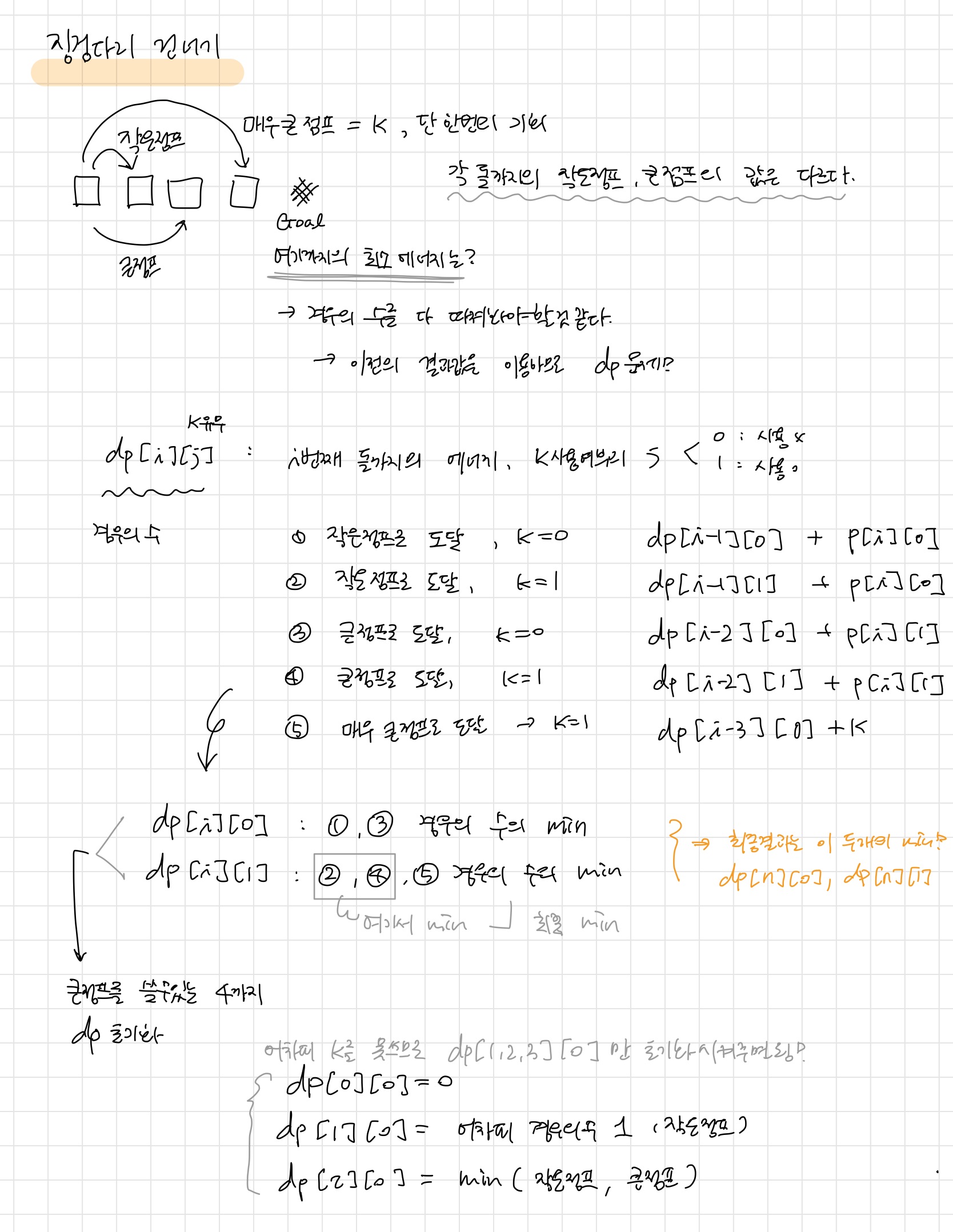
전형적인 dp문제이다.
각 돌에 도달하기 위한 값들을 잘 정리하면 풀 수 있다.
<코드>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define MAX 999999;
/*
three jumps
plus 1 (no skip)
plus 2 (1 skip)
plus 3 (2 skips) -> just one time & k energy
*/
int main(void)
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n,k; cin >> n;
pair<int, int> energy[21];
for(int i=1; i<n; i++) {
int x,y; cin >> x >> y;
energy[i] = make_pair(x,y);
}
cin >> k;
/*
dp[i][0]은 매우 큰 점프를 쓰지 않고 온 경우이다.
이 경우는 두가지 경로로 i번째까지 올 수 있는데
1. i-1번째에서 작은 점프 + i-1번째까지의 값
2. i-2번째에서 큰 점프 + i-2번째까지의 값
두가지 경우 중에서 최소값을 저장한다.
dp[i][1]은 매우 큰 점프를 i번째에 쓰고 온 경우이다.
이 경우 또한 두가지 경로로 i번째까지 올 수 있는데
1. 매우 큰 점프를 써서(k) i번째에 도달한 경우
2. i번째에 도달하기까진 다른 점프를 써서 오고, 그 전에 매우 큰 점프를 사용한 경우
두가지 경우 중에서 최소값을 저장한다.
이 중 2번째는 또 다시 경우의 수가 두가지로 나눠지는데,
이는 dp[i][0]을 구하는 방법과 같은 경우의 수이다.
1. i-1번째에서 작은 점프 + i-1번째까지의 값
2. i-2번째에서 큰 점프 + i-2번째까지의 값
다른 점은 그 전에 매우 큰 점프를 사용한 경우이므로 dp[?][1]의 값을 참조한다.
*/
int dp[21][2];
for (int i = 0; i <= n; i++) {
dp[i][0] = MAX;
dp[i][1] = MAX;
}
dp[1][0] = 0;
dp[2][0] = energy[1].first;
dp[3][0] = min(energy[1].first + energy[2].first, energy[1].second);
// 큰 점프를 쓸 수 있는 4번째 부터 n까지 반복문을 시작한다.
for(int i=4; i<=n; i++) {
dp[i][0] = min(energy[i-1].first + dp[i-1][0],
energy[i-2].second + dp[i-2][0]);
//cout << "dp[" << i-3 << "][0]" << dp[i-3][0] << endl;
dp[i][1] = min(k + dp[i-3][0],
min(energy[i-1].first + dp[i-1][1],
energy[i-2].second + dp[i-2][1]));
}
cout << min(dp[n][0], dp[n][1]);
return 0;
}728x90
'Algorithm > 백준과 프로그래머스' 카테고리의 다른 글
| [C++] 1991. 트리 순회 (0) | 2023.11.28 |
|---|---|
| [C++] 14940. 쉬운 최단거리 (2) | 2023.11.27 |
| [C++] 11508. 2+1세일 (0) | 2023.11.16 |
| [C++] 숫자짝궁 (0) | 2023.11.14 |
| [C++] 11286. 절댓값 힙 (0) | 2023.08.05 |